2. Modello Relazionale

Si basa sul concetto matematico di relazione: le relazioni hanno una rappresentazione naturale per mezzo di tabelle.

Relazione Matematica

Dati degli insiemi D1, D2, … Dn, il prodotto cartesiano $D_1 \times D_2 \times ... \times D_n$ è definito come l’insieme delle n-ple ordinate $(d_1, d_2, ..., d_n)$ tali che $d_1 \in D_1, d_2 \in D_2, ..., d_n \in D_n$ .

Si definisce relazione R un insieme tale che $R \subseteq D_1 \times D_2 \times ... \times D_n$ .

Si definiscono domini di R gli insiemi D1, D2, … Dn.

Il grado della relazione R è pari al numero di insiemi n coinvolti nel prodotto cartesiano.

Si definisce cardinalità di R il numero di n-ple di R.

Relazione nel Modello Relazionale

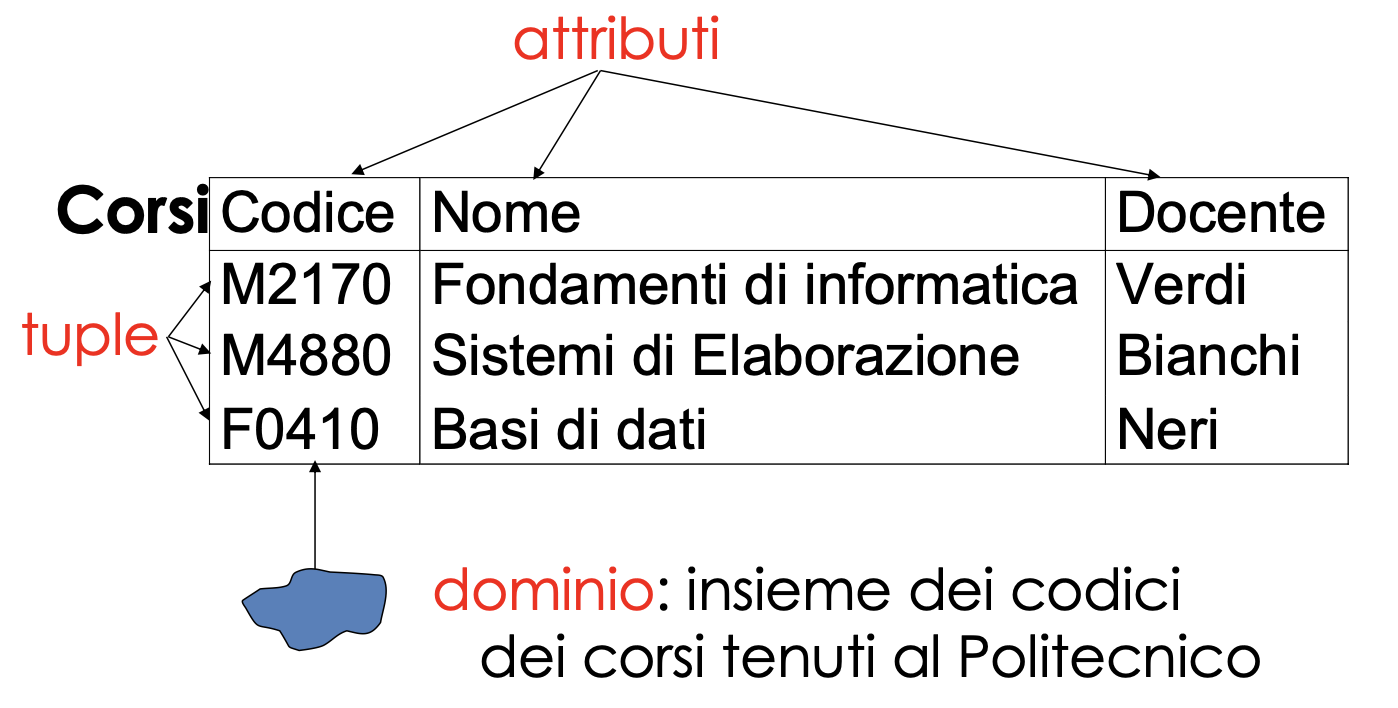
A ciascun dominio associamo un nome (attributo). L’ordinamento degli attributi non è rilevante: la struttura non è quindi posizionale.

L’associazione fra domini e attributi è definita da una funzione dom: Attr → D che associa a ciascun attributo possibile un dominio. Una n-pla (detta tupla) su un insieme di attributi X (sottoinsieme di Attr) è una funzione che associa a ciascun attributo A in X un valore del dominio dom(A). Una relazione su X è un insieme di tuple su X.

In parole povere: ogni colonna della tabella rappresenta un attributo; ogni riga della tabella è una tupla.

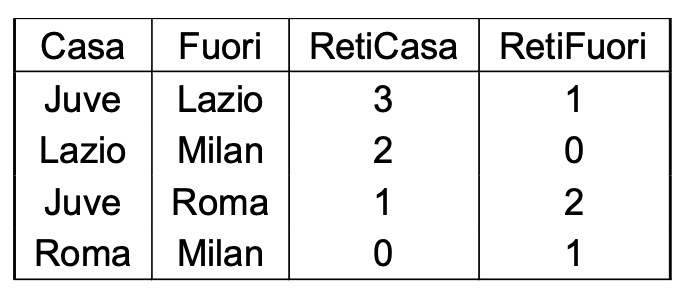
Se t è una tupla su X e $A \in X$ , allora $t[A]$ (oppure t.A) indica il valore di t su A.

Es: t[Squadra] = Lazio

Una tabella rappresenta una relazione se:

i valori di ciascuna colonna sono fra loro omogenei (dallo stesso dominio)

le righe sono diverse fra loro

le intestazioni delle colonne sono diverse tra loro (perciò i campi sono distinguibili mediante il loro nome e non la loro posizione)

Inoltre, in una tabella che rappresenta una relazione:

l’ordinamento tra le righe è irrilevante

l’ordinamento tra le colonne è irrilevante

Schema di una relazione: nome di una relazione R con un insieme di attributi… $R(A_1, A_2, ..., A_n)$ .

Schema di una base di dati: insieme di schemi di relazione con nomi diversi… $R= \{ R_1(X_1), R_2(X_2)... \}$ .

Istanza di una relazione su uno schema R(X): insieme r di tuple su X.

Identificazione delle tuple e chiavi

Si definisce chiave un insieme di attributi che identificano univocamente le tuple di una relazione. Es: matricola; dati anagrafici…

Un insieme K di attributi è superchiave per una relazione r se r non contiene due tuple distinte t1 e t2 tali che $t_1[K]=t_2[K]$ .

K è chiave per r se è una superchiave minimale (cioè non contiene un’altra superchiave) per r.

Ad esempio, nell’immagine sopra l’attributo Codice è chiave della relazione.

Teorema di esistenza delle chiavi

Ogni schema di relazione ha almeno una chiave.

Dim:

Poiché le relazioni sono insiemi, ogni relazione non può contenere tuple distinte ma uguali fra loro: 1. ogni relazione ha come superchiave l’insieme degli attributi su cui è definita. Perciò ogni schema di relazione ha almeno una chiave (l’insieme di tutti gli attributi o un suo sottoinsieme).

Valori nulli

A volte i dati possono essere mancanti: in questi casi si inserisce il valore null.

ATTENZIONE: in ogni tupla di una relazione non è consentito avere valori nulli per gli attributi che formano la chiave della relazione.

Vincolo di integrità referenziale

Informazioni in relazioni diverse sono correlate attraverso valori comuni, in particolare tramite i valori delle chiavi.

Un vincolo di integrità referenziale fra un insieme di attributi X di una relazione R1 e un’altra relazione R2 impone ai valori su X di ciascuna tupla dell’istanza di R1 di comparire come valori della chiave (primaria) dell’istanza di R2.